
SOFTWARE
Click on the link below to download a Wavelet CODEC program.
The program will compress/decompress full color (24 bit) and Mono (8bit) bitmap images.
(16 and 32 bit color are not supported)
You can view the original uncompressed image and compressed image side by side to examine the effects of the compression (Use tile windows)
The zipped file contains an executable Wcomp.exe and a DLL WAV1.dll. Just place them in the same folder. Nothing is installed, so to remove the programs, just delete them.
WAVELET CODEC PROGRAM (Zipped file containing Wcomp.exe and WAV1.dll).
Click on the link below to download a Wavelet CODEC program.
The program will compress/decompress full color (24 bit) and Mono (8bit) bitmap images.
(16 and 32 bit color are not supported)
You can view the original uncompressed image and compressed image side by side to examine the effects of the compression (Use tile windows)
The zipped file contains an executable Wcomp.exe and a DLL WAV1.dll. Just place them in the same folder. Nothing is installed, so to remove the programs, just delete them.
WAVELET CODEC PROGRAM (Zipped file containing Wcomp.exe and WAV1.dll).


WAVELET COMPRESSION
ORIGINAL PICTURE (standard Lena)
TWO LEVEL DECOMPOSITION
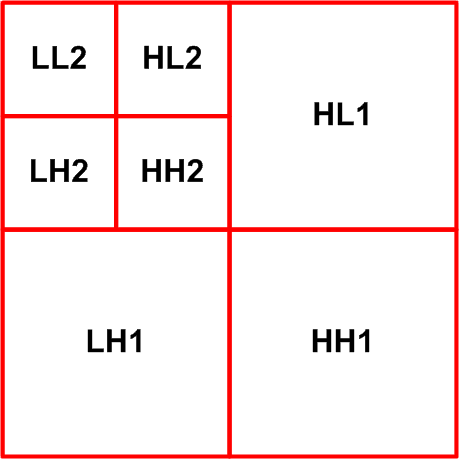
DECOMPOSITION MAP

The discrete wavelet transform is a hierarchical subband technique where the subbands are logarithmically spaced in frequency and represent an octave-band decomposition. To start the decomposition, the image is filtered in both the horizontal and vertical directions using separable filters. This creates four subbands as follows:
Subband LL1 represents the horizontal and vertical low frequency components of the image
Subband HH1 represents the horizontal and vertical high frequency components of the image
Subband LH1 represents the horizontal low and vertical high frequency components
Subband HL1 represents the horizontal high and vertical low frequency components
To obtain the next level in the decomposition the two filters are again applied, but only to the LL1 subband. Again we obtain four subbands labeled LL2, HH2, LH2, and HL2 with representations similar to the first level subbands.
The following example illustrates the discrete wavelet transform using 9 tap symmetrical quadrature mirror filters. Some of the subbands have been amplified to show the details.
Subband LL1 represents the horizontal and vertical low frequency components of the image
Subband HH1 represents the horizontal and vertical high frequency components of the image
Subband LH1 represents the horizontal low and vertical high frequency components
Subband HL1 represents the horizontal high and vertical low frequency components
To obtain the next level in the decomposition the two filters are again applied, but only to the LL1 subband. Again we obtain four subbands labeled LL2, HH2, LH2, and HL2 with representations similar to the first level subbands.
The following example illustrates the discrete wavelet transform using 9 tap symmetrical quadrature mirror filters. Some of the subbands have been amplified to show the details.